你是否曾对数学中的“正交”和“斜交”感到困惑?它们究竟意味着什么?今天,就让我们一起深入探索这两个概念,从几何图形到向量空间,从物理学到计算机科学,全方位解析它们的含义和应用。准备好了吗?让我们开始这场知识的冒险之旅!
一、几何世界中的正交与斜交
想象你站在一个充满线条和角度的几何世界里。正交和斜交,这两个词最初就源于几何学。在欧几里得几何中,正交指的是两条直线或平面相交时形成的直角,也就是90度角。而斜交则是指两条直线或平面相交时形成的非直角,即小于或大于90度的角。
在现实生活中,我们随处可见正交和斜交的例子。比如,房间的墙壁和地面通常是正交的,因为它们形成90度角。而楼梯的踏板和扶手则可能是斜交的,因为它们形成的是锐角或钝角。
二、向量空间中的正交与斜交
当你进入更深层次的数学领域,你会发现正交和斜交的概念不仅仅局限于几何图形。在向量空间中,正交和斜交同样具有重要意义。
在向量空间中,两个向量如果它们的点积(内积)为零,那么这两个向量就是正交的。换句话说,它们的夹角是90度。例如,在三维空间中,向量(1, 0, 0)和向量(0, 1, 0)就是正交的,因为它们的点积为0。
而斜交则是指两个向量的点积不为零,即它们的夹角不是90度。比如,向量(1, 1, 0)和向量(0, 1, 1)就是斜交的,因为它们的点积不为0。
三、物理学中的正交与斜交
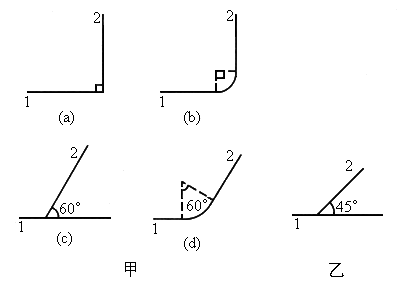
在物理学中,正交和斜交的概念同样无处不在。比如,在力学中,力的分解和合成常常涉及到正交和斜交的概念。当你将一个力分解成两个互相垂直的分力时,这两个分力就是正交的。
在电磁学中,电场和磁场也是正交的。电场线和磁场线通常垂直相交,形成电磁波。这种正交关系在电磁波的传播中起着至关重要的作用。
四、计算机科学中的正交与斜交
在计算机科学中,正交和斜交的概念同样有着广泛的应用。在图形学中,正交坐标系是描述二维和三维空间的基础。而斜交坐标系则用于描述非正交的空间,比如在地图投影中,不同的投影方式可能会导致经纬线形成斜交关系。
在数据挖掘和机器学习中,正交和斜交的概念也经常出现。比如,主成分分析(PCA)就是一种通过正交变换将高维数据降维到低维空间的方法。而线性回归中,自变量和因变量之间的关系也可能是斜交的,需要通过适当的变换使其变为正交关系。
五、正交与斜交的实际应用案例
让我们来看一些具体的实际应用案例,进一步理解正交和斜交的意义。
1. 建筑结构设计:在建筑结构设计中,正交和斜交的概念被广泛应用于梁、柱、墙等结构的设计中。比如,梁和柱通常形成正交关系,以确保结构的稳定性。而楼梯的踏板和扶手则可能是斜交的,以提供更好的使用体验。
2. 导航系统:在导航系统中,正交坐标系是描述地理位置的基础。而斜交坐标系则用于描述不同地理坐标系之间的关系,比如在地图投影中,不同的投影方式可能会导致经纬线形成斜交关系。
3. 医学影像处理:在医学影像处理中,正交和斜交的概念同样具有重要意义。比如,在CT扫描中,扫描平面通常是正交的,以获取清晰的图像。而在MRI中,磁场和射频脉冲的施加方向可能是斜交的,以获得更丰富的信息。
通过这些案例,我们可以看到正交和斜交的概念在各个领域的广泛应用,它们不仅是数学和物理学的抽象概念,更是解决实际问题的有力工具。
通过今天的探索,你是否对正交和斜交有了更深入的理解?从几何图形到向量空间,从物理学到计算机科学,正交和斜交的概念贯穿于各个领域,它们不仅是数学和物理学的抽象概念,更是解决实际问题的有力工具。希望今天的探索能让你在知识的海洋中收获更多,也期待你在未来的学习和工作中,能更好地运用这些概念,解决更多的问题。





